¿Cómo se evalúan los modelos de Machine Learning en el sector sanitario?

Una de las grandes preocupaciones para los profesionales del sector sanitario a la hora de afrontar proyectos que emplean técnicas de Machine Learning es cómo se evalúan estos modelos para ser fiables y conseguir la eficacia clínica deseada.

Existen distintas formas de evaluación que dependen sobre todo del tipo de problema que estemos tratando de resolver. Entre los más comunes destacamos los problemas de regresión y de clasificación, ambos perteneciente a la rama de Machine Learning conocida como aprendizaje supervisado.

Los problemas de regresión se caracterizan por tener una variable respuesta Y cuantitativa, es decir, la solución a nuestro problema es representada por un variable continua. Ej: la estancia de un paciente. Mientras que los problemas de clasificación se caracterizan por tener una variable respuesta Y cualitativa o categórica, es decir, la solución a nuestro problema va a predecir la categoría a la que pertenece una nueva observación. Ej: presencia de una enfermedad.

Dependiendo del tipo de problema a resolver nos vamos a encontrar distintos métodos de evaluación. En este artículo vamos a tratar de analizar los diferentes métodos de evaluación que conllevan los modelos de clasificación, por ser lo que presentan una mayor complejidad para ser evaluados.

Matriz de confusión

Un modelo de clasificación es aquel capaz de predecir a qué clase va a pertenecer una instancia, basándose en lo aprendido en datos pasados. Así, en un modelo binario, podemos considerar dos clases: “Positiva” (por ejemplo, presencia de una enfermedad) y “Negativa” (por ejemplo, ausencia de dicha enfermedad).

Para evaluar estos modelos es necesario tener en cuenta los tipos de predicciones correctas e incorrectas que realiza el modelo clasificador. Es aquí donde entra en juego la Matriz de Confusión.

La matriz de confusión de un problema de n clases es una matriz nxn en la que las filas se nombran según las clases reales, y las columnas según las clases previstas por el modelo.

Sirve para mostrar de forma explícita cuándo una clase es confundida con otra. Por eso, permite trabajar de forma separada con distintos tipos de error. 

Por ejemplo, en un modelo binario que busque predecir la presencia de una determinada enfermedad (1) o la ausencia de esta (0), la matriz de confusión correspondiente sería:

De esta forma la diagonal principal contiene la suma de todas las predicciones correctas, mientras que la otra diagonal refleja los errores del clasificador.

Sin embargo, una limitación es que cuando queremos comparar entre dos modelos este método es muy poco intuitivo.

Cuando la importancia radica en problemas sanitarios, cómo predecir la presencia o ausencia de una determinada enfermedad, el error tipo I y tipo II tienen distinto peso. Es decir, no es lo mismo diagnosticar una enfermedad a un paciente sano (Error tipo I) que dejar de diagnosticar una enfermedad a un paciente enfermo (Error tipo II).   Normalmente, el error tipo II debería penalizarse en mayor medida en este caso.

Viendo la importancia que tiene discriminar en cada caso concreto los distintos tipos de error que puedan resultar de la aplicación de algoritmo, entendemos mejor la necesidad de trabajar con diferentes métricas.

A partir de la matriz de confusión podemos obtener nuevas métricas cómo:

• Exactitud 

La exactitud es la fracción de predicciones que el modelo clasifica correctamente.

Exactitud = (VP + VN) / N

Siendo N el número total de predicciones.

La gran limitación es que cuando las clases a categorizar están muy desequilibradas este método resulta poco útil. 

• Precisión 

La precisión es el ratio o porcentaje de clasificaciones correctas de nuestro modelo clasificador dentro de las predicciones positivas. 

Precisión = VP / (VP + FP)

• Sensibilidad 

La sensibilidad es la proporción de pacientes que se identificaron correctamente por tener una condición, verdadero positivo, sobre el número total de pacientes que realmente presentan esa condición.

Sensibilidad = VP / (VP + FN)

• Especificidad

La especificidad es la proporción de pacientes que se identificaron correctamente por no tener una condición, verdadero negativo, sobre el número total de pacientes que realmente no presentan esa condición.

Especificidad = VN / (VN + FP)

La conveniencia de usar una métrica u otra como medida del estimador dependerá de cada caso en particular y del “coste” asociado a cada error de clasificación del algoritmo. 

Otra opción que puede ser bastante apropiada es, si se dispone del suficiente conocimiento experto, crear tu propia métrica, dando pesos a las cuatro celdas de la matriz de confusión. Estas son métricas estándar, pero si se conoce bien el problema crear una métrica ajustada manualmente puede ser más adecuado.

Sin embargo, existen gráficos que consiguen relacionar las distintas métricas entre sí con el fin de obtener un método de evaluación fiable.

Curva precisión-sensibilidad

Esta curva es el resultado de dibujar la gráfica entre la precisión y la sensibilidad. Nos permite ver a partir de qué sensibilidad tenemos una degradación de la precisión y viceversa. Lo ideal de esta curva es que se acerque lo máximo posible a la esquina superior derecha (alta precisión y alta sensibilidad). 

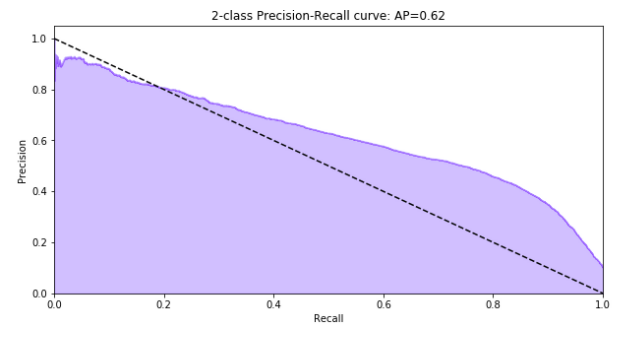
Figura 1. Ejemplo de Curva Precisión vs. Sensibilidad.

Además, se obtiene el valor de precisión media (área bajo la curva) que nos sirve para comparar el rendimiento de diferentes curvas. Cuanto más se acerque el valor de esta área a 1, mejor será el modelo.

Curva ROC

Uno de los métodos más usados en el ámbito sanitario para evaluar el rendimiento en problemas de clasificación es la curva ROC (Característica de Funcionamiento del Receptor).

La curva ROC nos indica con qué precisión es capaz de distinguir el modelo entre dos clases a través de un gráfico. 

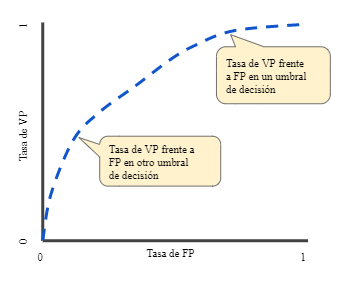
Figura 2. Ejemplo de Curva ROC: VPR (Sensibilidad)  vs. FPR( 1- Especificidad).

Esta curva representa la sensibilidad (o tasa de verdaderos positivos) frente a la especificidad (o tasa de verdaderos negativos). La evaluación de los métodos mediante la curva ROC tiene en cuenta la relación entre la sensibilidad del modelo y la detección de falsos positivos.

En las curvas ROC, interesa que la curva se acerque lo máximo posible a la esquina superior izquierda de la gráfica, de manera que el hecho de aumentar la sensibilidad no haga que nuestro modelo introduzca más falsos positivos. 

Además, a partir de estar curvas, se obtiene el área bajo la curva (AUC) que nos sirve como métrica para resumir la curva y poder comparar modelos. Al igual que el valor de precisión media, cuanto más se acerque el valor del AUC al 1, mejor será el modelo.