Ganancia clínica de modelos predictivos
Análisis predictivo
Los modelos predictivos consisten en el empleo de técnicas, como Machine Learning, para identificar patrones en los datos y poder predecir resultados a partir de estos.
Estos modelos se pueden utilizar para predicciones de todo tipo. En concreto, en sanidad, podría emplearse por ejemplo para prevenir la readmisión de los hospitales. Reducir las readmisiones hospitalarias no sólo mejora la satisfacción del paciente sino que supondría un gran ahorro para los hospitales. Los modelos predictivos pueden emplearse para identificar pacientes con alto riesgo de readmisión tras un diagnóstico/tratamiento particular y orientar sobre cuándo organizar un seguimiento y las instrucciones óptimas para evitar la readmisión.
Hasta ahora los modelos predictivos se evaluaban con medidas de precisión tradicionales, como la Curva ROC, que sólo tienen en cuenta la precisión de diagnóstico del modelo predictivo, pero fallan a la hora de evaluar la utilidad clínica del modelo. Con el fin de resolver este problema, surgen nuevos métodos como la curva de decisión y los ensayos aleatorizados.
Curva de decisión
La curva de decisión es una técnica que se emplea para la evaluación de modelos predictivos, especialmente para comparar test diagnósticos en el ámbito clínico. La ventaja de esta técnica es que integra información clínica adicional.
Las métricas tradicionales, como la curva ROC, nos dan un valor de corte que a menudo no es preciso para su aplicación técnica. Estas medidas de evaluación sólo tienen en cuenta la precisión de diagnóstico de la predicción de un modelo frente a otro, sin llegar a tener en cuenta la utilidad clínica del modelo específico. Por lo tanto, las curvas de decisión, surgen como alternativa a estas medidas de evaluación tradicionales.
Uno de los conceptos clave de las curvas de decisión es el umbral de probabilidad, . Este se correspondería al momento donde el beneficio esperado de un tratamiento es igual al beneficio esperado de evitar el tratamiento. Es decir, es a partir de este valor cuándo el tratamiento se considera beneficioso. El umbral de probabilidad varía dependiendo de cada individuo. Este umbral permite analizar cuando un modelo es mejor que otro para cierto rango de umbrales de probabilidad, con respecto al beneficio neto.
Para comparar dos modelos en un determinado umbral de probabilidad, se calcula el beneficio neto con la siguiente ecuación:
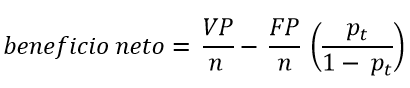
Donde VP y FP son los verdaderos positivos y falsos positivos, respectivamente, n el número de sujetos y pt la probabilidad umbral.
Suponiendo que queremos comparar dos modelos para predecir/diagnosticar una enfermedad, para cada paciente habrá una probabilidad predicha de padecer la enfermedad basada en los modelos. Entonces los pacientes con una probabilidad de padecer la enfermedad superior al umbral de probabilidad tendrán un diagnóstico positivo, y los pacientes con probabilidad de padecer la enfermedad menor al umbral de probabilidad tendrán un diagnóstico negativo. Por lo que concluiremos que un modelo es mejor que otro para cierta probabilidad umbral cuando el beneficio neto sobrepase el beneficio neto del otro modelo para cierto valor , y que un modelo es superior a otro de forma global si su beneficio neto total para todos los posibles valores de , también conocido como el área bajo la curva de decisión, es mayor.
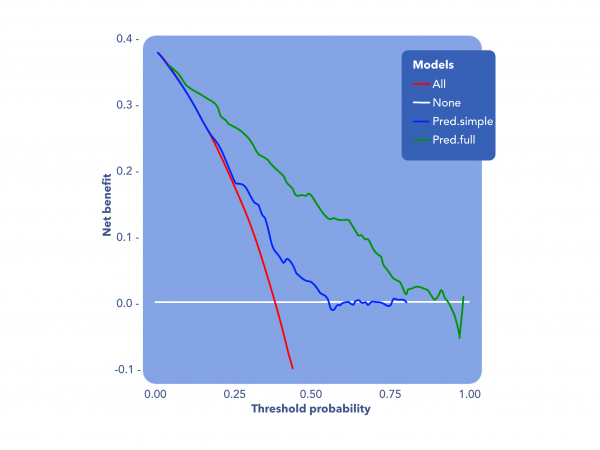
Ejemplo de análisis de curvas de decisión para varios modelos.
Ensayos aleatorizados
Normalmente, la significancia clínica de un tratamiento se demuestra en ensayos clínicos aleatorizados en los que se evalúan sus efectos comparando el resultado obtenido en dos grupos de pacientes. En uno de ellos ―el grupo experimental― se aplica el tratamiento o factor testeado, mientras que en el otro ―el grupo de control― no se aplica dicho factor. De esta forma se analizan las diferencias, tanto positivas como negativas, observadas en el grupo experimental frente al grupo de control para evaluar el factor testeado.
Estos ensayos nos proporcionan información clínica de dos maneras distintas: por la presencia de efectos secundarios y por la evaluación clínica de los beneficios de un tratamiento frente al control. No obstante, esta información siempre se valora por las diferencias entre ambos grupos.
Por lo tanto, una alternativa con la que obtener información más precisa sería la evaluación a nivel individual a partir de un modelo predictivo. Este método consiste en realizar predicciones individuales para cada paciente del grupo experimental con las que podremos asignar un tratamiento u otro dependiendo de ciertos valores de variables clínicas de cada paciente. Esta aproximación estima la diferencia en el resultado de ambos tratamientos para cada individuo donde la decisión de que tratamiento aplicar está basada en el modelo predictivo con la que elegir el tratamiento más adecuado para cada individuo. De este modo, estaríamos hablando de un ensayo aleatorizado clásico, pero donde el factor testeado sería el propio modelo predictivo.
Referencias:
Zhang Z, Rousson V, Lee W. (2018). Decision curve analysis: a technical note. Ann Transl Med; 6(15):308.
Kattan M, Sarget D. (2007). Method for evaluating prediction models that apply the results of random trials to individual patients. Trials; 8:14.



